Formule de la hauteur dans le triangle et Formule de Héron
Pour la 1ère S.
Voici une application de la formule d'Al-Kashi : on obtient une expression donnant la longueur d'une hauteur en fonction des côtés du triangle.
On en déduit la formule (dite de Héron) qui donne l'aire du triangle en fonction des côtés.
Note :
On suppose connue la loi des cosinus (formule d’Al-Kashî) :
Théorème 1 (Loi des cosinus).
Dans tout triangle ABC,
Cette relation permet de calculer la longueur d’une hauteur à partir de celles des côtés.
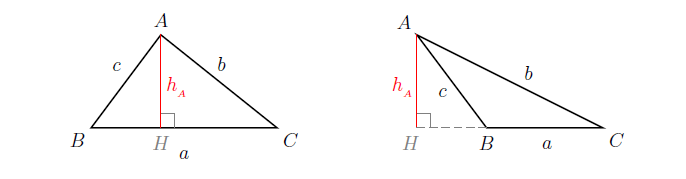
Théorème 2
Dans un triangle ABC, le segment de hauteur issue de est donné en fonction de côtés , , par
où désigne le demi-périmètre .
Démonstration
Avec la loi des cosinus, on a :
.
Par projection de sur , on a :
.
D’où
.
On a donc : .
Dans le triangle ABH, le théorème de Pythagore donne donc
= .
Pour obtenir une expression plus « lisible », on fait apparaître une différence de deux carrés :
;
la factorisation par l’identité donne
.
Avec les identités , on a
L’identité donne encore
.
En observant la symétrie des différents facteurs du numérateur, on écrit
Avec le demi-périmètre
,
On a donc :
.
On en déduit finalement
= .
Corollaire 1.
L’aire du triangle est donnée par :
.
Démonstration.
En effet, l’aire est donnée par :
.
Aller plus loin sur les triangles
Pour poursuivre sur les théorèmes liés aux triangles, consultés également ces autres fiches conseils sur notre site :
- Les théorèmes de géométrie dans les triangles
- Le calcul de l'aire ou de la surface d'un triangle rectangle
- Les triangles en cinquième
- Les angles et les parallèlismes
Vous pouvez également vous en référer à ce site pour savoir Comment construire la hauteur d'un triangle.
Calculer l'aire d'un triangle
En complément de cet article sur la hauteur du triangle, vous pouvez aussi avoir à calculer l'aire d'un triangle (en l'occurrence un triangle rectangle.
Dans ce cas, nos fiche-méthode, vous donnerons une courte introduction sur les propriétés du triangle rectangle, la formule générale pour calculer l'aire d'un triangle quelconque, la formule particulière du calcul de la surface d'un triangle rectangle et d'un triangle rectangle isocèle et des exercices.
Alors, comment faire pour calculer rapidement et facilement l'aire (également appelée surface) d'un triangle rectangle ?
Propriétés du triangle rectangle
Un triangle rectangle est un triangle dont l'un des angles est droit.
Un triangle rectangle est caractérisé par :
- 3 sommets et 3 côtés comme un triangle classique
- 1 angle droit
- 1 des côtés non adjacent à cet angle droit appelé hypothénuse
- 1 hauteur issue de l'angle droit du triangle notée hh
La formule généralement utilisée pour calculer l'aire (également appelée surface) d'un triangle quelconque :
avec :
- l'aire en
- la base du triangle en cm
- la hauteur du triangle en cm
Par Zauctore
Toutes nos vidéos sur formule de la hauteur dans le triangle