Quelques rappels
I. Ensembles de nombres.
1. Les entiers naturels et relatifs.
Il existe différents ensembles de nombres.
Le premier que nous rencontrons dans notre scolarité (ou notre vie) est bien sûr l'ensemble des entiers naturels, que l'on note . C'est l'ensemble des nombres 1, 2, 3, 561...
Cet ensemble paraît suffisant pour résoudre de nombreux problèmes. Il en existe un pour lesquels les nombres naturels ne suffisent plus.
Trouver un nombre qui, ajouté à 5 donne 2.
Ce problème peut se reformuler grâce à une équation de la manière suivante :
où est notre nombre inconnu.
L'idée de construire des nombres qui seraient solutions de cette équation a émergé. Ces nombres solutions s'appellent les nombres négatifs.
Ils s'écrivent à l'aide du signe .
La solution du problème est donc .
L'ensemble des entiers positifs et négatifs s'appelle les entiers relatifs, et se note .
2. Les nombres décimaux et rationnels.
L'aventure pourrait s'arrêter là.
Cependant, il existe un autre problème pour lequel les nombres actuellement disponibles ne conviennent pas.
Trouver un nombre qui multiplié par 5 donne 41.
Ce problème peut se reformuler grâce à une équation de la manière suivante :
Aucun des nombres que nous avons à notre disposition ne convient.
L'idée de construire des nombres qui seraient solutions de cette équation a, là aussi, émergé. Ces nombres solutions s'appellent les nombres rationnels.
Ils s'écrivent sous la forme d'une fraction. Ici, la solution s'écrira
Il existe deux sortes de nombres rationnels : les nombres décimaux et les nombres rationnels (non décimaux).
La différence est simple :
- les nombres décimaux sont des nombres dont l'écriture peut être une fraction ayant un dénominateur égal à 10. Par exemple, le nombre solution de notre problème est un nombre décimal :
- les nombres rationnels non décimaux, que l'on nommera seulement par rationnels, n'ont pas d'écriture décimale finie. Par exemple, le nombre n'a pas d'écriture décimale finie (ce nombre vaut environ .
L'ensemble des nombres décimaux s'écrit alors que l'ensemble des nombres rationnels s'écrit .
On remarque facilement que n'importe quel nombre décimal est un nombre rationnel.
On écrit alors :
3. Les nombres réels.
L'aventure ne s'arrête pas là. Nous pouvons trouver un autre problème que les nombres connus jusqu'à présent ne résolvent pas.
Trouver un nombre tel que son carré vaut 2.
Ce problème peut se reformuler grâce à une équation de la manière suivante :
Nous avons au départ pensé que le nombre solution était une fraction. Il n'en est rien. Pour vous en convaincre, je vous laisse lire la démonstration qui se trouve dans une des pages du site : est irrationnel
Il existe donc de nouveaux nombres, appelés nombres réels qui permettent de résoudre ce problèle. Leur ensemble s'écrit .
Les nombres réels n'ont pas de forme particulière. Il en existe une infinité, comme ou .
On peut imaginer qu'il n'en existe pas d'autre. Il existe cependant des problèmes qui n'admettent pas de solutions réelles.
4. Les nombres complexes.
Le problème est le suivant :
Trouver un nombre dont le carré est .
Ce problème n'a bien sur pas de solution réelle : il n'existe aucun nombre réel qui au carré donne .
Ces solutions existe cependant, on les appelle les nombres complexes et leur ensemble est noté .
Leur étude s'arrêtera ici pour l'instant, elle relève de la classe de terminale S.
La construction de tous ces ensembles n'est pas au programme du lycée. Les démonstrations font appel à des notions bien complexes et demandent une aisance technique que l'on apprend au lycée notamment.
On peut cela dit en donner une propriété :
II. Pour les équations.
1. Identités remarquables.
Propriété :
Quelque soient les réels et , on a :
Si on utilise cette égalité de gauche à droite, on s'en servira pour développer.
Si on utilise cette égalité de droite à gauche, on s'en servira pour factoriser.
2. Le théorème produit.
Théorème :
Un produit de facteurs est nul si et seulement si l'un des facteurs est nul.
Remarque :
Pour tous réels et ,
3. Le théorème quotient.
Théorème :
Un quotient de facteurs est nul si et seulement si le dénominateur est non nul et le numérateur est nul.
Autrement dit,
III. Signes et inéquations.
1. Signe de .
Propriété :
Si et sont deux réels et , alors change de signe pour la valeur qui l'annule.

2. Signe d'un produit.
Faisons un exemple.
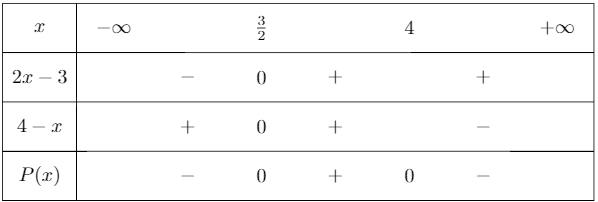
On considère
On résous alors :
Ainsi,
On a le tableau de signe suivant :
3. Signe d'un quotient.
Faisons un exemple.
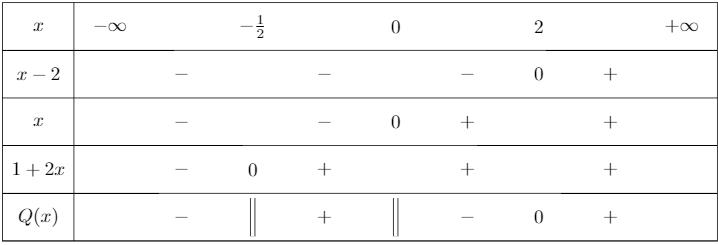
On considère
La première question à se poser est la suivante : "Pour quelle valeur de la fonction existe-t-elle ?"
Donc existe pour et .
est donc définie sur
On dit alors que est l'ensemble de définition de .
Dressons alors son tableau de signes.
Pour cela, résolvons quelques équations.
On peut maintenant dresser son tableau de signes.
4. Résoudre une inéquation.
Dès que l'on doit résoudre une inéquation, on dresse un tableau de signe.
Résoudre dans l'inéquation :
L'inéquation est définie sur car
Sur cet ensemble de définition, l'inéquation est équivalente à :
Il n'y a qu'une valeur qui annule cette fraction :
Dressons son tableau de signe :
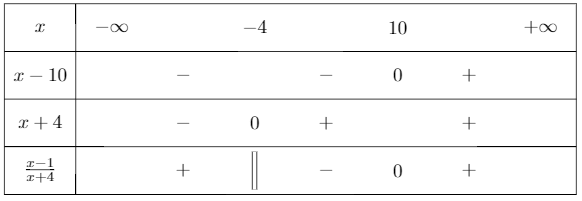
Ainsi,
Toutes nos vidéos sur rappels pour une 1ère s