Les suites en 1ère S

I. Premières définitions

Définition :
Soit n0n_0 un entier naturel. Une suite uu est une fonction associant à tout entier naturel n≥n0n\geq n_0 un réel u(n)u(n) que l'on va noter unu_n.

Notation :
La suite u est parfois notée (un)(u_n) ou (un)n≥n0(u_n)_{n\geq n_0}.
Si on ne parle que de la suite (un)(u_n), on sous-entend que n∈Nn\in\mathbb N.

Vocabulaire :
Le réel unu_n est appelé terme d'indice nn de la suite uu.

On peut définir une suite de deux manières différentes :

Définition explicite

Soit n0n_0 un entier naturel. Une suite (un)n≥n0(u_n)_{n\geq n_0} est définie de façon explicite lorsqu'il existe une fonction ff définie sur [n0 ; +∞[[n_0\ ;\ +\infty[] telle que :
pour tout entier n≥n0n\geq n_0, un=f(n)u_n=f(n).

Remarque :
Le terme f(n)f(n) est aussi appelé terme général de la suite.

Exemple :
La suite (un)(u_n) définie pour tout n∈Nn\in\mathbb N par un=3n2+7u_n=3n^2+7 est définie de façon explicite et sa fonction associée est f(x)=3x2+7f(x)=3x^2+7

Définition par récurrence

Soit un0u_n0 un entier naturel. Une suite (un)n≥n0(u_n)_{n\geq n_0} est définie par récurrence lorsque le premier terme u_n_0 est donnée et qu'il existe une fonction ff telle que :
pour tout entier n≥n0n\geq n_0, un+1=f(un)u_{n+1}=f(u_n).

Exemple :
La suite (un)(u_n) définie pour n∈Nn\in\mathbb N par {un+1=5un+9u0=4\begin{cases} u_{n+1}=5u_n+9 \\ u_0=4\end{cases} est une suite définie par récurrence et la fonction associée est définie par f(x)=5x+9f(x)=5x+9 pour x∈Rx\in\mathbb R.

Différences entre les deux définitions

  • Lorsqu'une suite est définie de façon explicite, on peut calculer directement le terme unu_n.
  • Lorsqu'une suite est définie par récurrence, pour calculer le neˋmen^{ème} terme, il faut calculer tous les termes précédents.

II. Représentation graphique d'une suite

Tout comme les fonctions, les suites peuvent se représenter graphiquement. Nous allons séparer ce paragraphe en deux parties, suivant les deux définitions différentes des suites : façon explicite et par récurrence.

1. Suite définie de façon explicite.

Soit ff une fonction définie sur [0 ; +∞[\lbrack0\ ;\ +\infty\lbrack et (un)(u_n) la suite définie sur N\mathbb N par un=f(n)u_n=f(n).
Pour représenter graphiquement la suite (un)(u_n), il suffit de calculer les termes de la suite et de placer les points de coordonnées (n ; un)(n\ ;\ u_n).

Exemple :
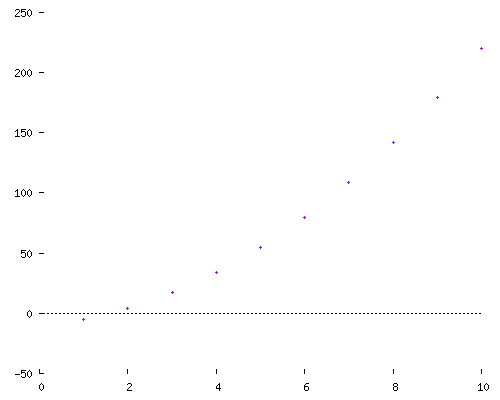
On représente graphiquement la suite définie par :
un=2n2+3n−10u_n=2n^2+3n-10.
On place les points de coordonées (0 ; −10)(0\ ;\ -10), (1 ; −5)(1\ ;\ -5), (2 ; 4)(2\ ;\ 4)...
graphique-suite-numérique

2. Suite définie par récurence.

Pour cette partie, cliquer sur le lien suivant : représentation graphique de suites définies par récurrence

3. Variations d'une suite.

Tout comme les fonctions, on peut parler de variations de suites.

Défintion :
Soit n0n_0 un entier naturel et (un)n≥n0(u_n)_{n\geq n_0} une suite de réels.
On dit que la suite (un)n≥n0(u_n)_{n\geq n_0} est croissante lorsque, pour tout entier n≥n0n\geq n_0, un+1≥unu_{n+1}\geq u_n.
On dit que la suite (un)n≥n0(u_n)_{n\geq n_0} est décroissante lorsque, pour tout entier n≥n0n\geq n_0, un+1≤unu_{n+1}\leq u_n.
On dit qu'une suite est monotone lorsqu'elle est croissante ou décroissante.

Intéressons nous maintenant à deux exemples de suites importantes au lycée : les suites arithmétiques et les suites géométriques.

III. Suites arithmétiques

1. Définition.

Soit unu_n une suite de réels et rr un réel. La suite (un)(u_n) est dite artihmétique de raison rr si elle vérifie :
pour tout n∈Nn\in\mathbb N, un+1=un+ru_{n+1}=u_n+r

Remarque :
Une suite arithmétique n'est finalement rien d'autre qu'une suite obtenue en ajoutant le nombre rr à un terme de la suite pour obtenir le terme suivant.

2. Propriétés.

Propriété : forme explicite d'une suite arithmétique.
Soit rr un réel et (un)(u_n) une suite arithmétique de raison rr.
Pour tout entier naturel nn, on a :

un=u0+nru_n=u_0+nr

De manière générale, si pp est un entier naturel, on a :

un=up+(n−p)ru_n=u_p+(n-p)r

Remarque :
On peut se donner une démonstration un peu "intuitive du résultat", il suffit de calculer les premiers termes de la suite en prenant en compte la remarque précédente :

u1=u0+ru_1=u_0 +r

u2=u1+r=u0+r+r=u0+2ru_2=\textcolor{red}{u_1} +r=\textcolor{red}{u_0+r}+r=u_0+2r

u3=u2+r=u0+2r+r=u0+3ru_3=\textcolor{red}{u_2} +r=\textcolor{red}{u_0+2r}+r=u_0+3r

u4=u3+r=u0+3r+r=u0+4ru_4=\textcolor{red}{u_3} +r=\textcolor{red}{u_0+3r}+r=u_0+4r

... et ainsi de suite, de manière à trouver la formule générale.

Propriété : variations d'une suite arithmétique.
Soit rr un réel et (un)(u_n) une suite arithmétique de raison rr.

  • Si r>0r>0, alors la suite est croissante ;
  • Si r<0r<0, alors la suite est décroissante ;
  • Si r=0r=0, alors la suite est constante.

3. Somme des premiers termes d'une suite arithmétique.

Théorème :
Soit nn un entier naturel différent de 0. On a alors :

1+2+3+...+n=n(n+1)21+2+3+...+n=\frac{n(n+1)}{2}

Exemple :
La somme des 100 premiers termes entiers est donnée par le calcul :

1+2+3+...+100=100×1012=5 0501+2+3+...+100=\frac{100\times 101}{2}=5\ 050

Une petite remarque sur ce calcul : une histoire raconte que lorsque le mathémticien Carl Friedrich Gauss était enfant, son maître à l'école primaire aurait demandé à la classe, pour les calmer de leur agitation du moment, de faire la somme des nombres entiers de 1 à 100, pensant qu'il serait tranquille pendant un bon moment. Gauss aurait alors proposé une réponse très vite, provoquant la stupéfaction de son maître d'école !
La méthode utilisée était sensiblement basée sur la formule précédente : il aurait écrit les nombres de 1 à 100 dans un sens, puis sur la ligne dessous dans l'autre sens. Il a ainsi dû faire les 100 sommes 1+100, 2+99, 3+98, 4+97... et remarquer que le résultat était toujours le même : 101.
Remarquant qu'il venait de calculer deux fois la somme en question, il en prit la moitié :

100×1012=5 050.\frac{100\times 101}{2}=5\ 050.

Et ce à l'âge de 8 ou 9 ans... C'était le début d'une grande carrière dans les mathématiques, qui lui vaudra le surnom de "prince des mathématiques".
Refaites le procédé sur une feuille pour vous en convaincre !

Théorème :
Soit rr un réel et (un)(u_n) une suite arithmétique de raison rr.
Soit nn un entier naturel. On a alors :

u0+u1+...+un⎵n+1 termes=(n+1)×u0+un2\underbrace{u_0+u_1+...+u_n}_{n+1 \textrm{\ termes}}=(n+1)\times\frac{u_0+u_n}{2}

IV. Suites géométriques.

1. Définition.

Soit unu_n une suite de réels et qq un réel non nul. La suite (un)(u_n) est dite géométrique de raison qq si elle vérifie :
pour tout n∈Nn\in\mathbb N, un+1=un×qu_{n+1}=u_n\times q

Remarque :
Une suite géométrique n'est finalement rien d'autre qu'une suite obtenue en multipliant le nombre qq à un terme de la suite pour obtenir le terme suivant.

2. Propriétés.

Propriété : forme explicite d'une suite géométrique.
Soit qq un réel et (un)(u_n) une suite géométrique de raison qq.
Pour tout entier naturel nn, on a :

un=u0×qnu_n=u_0\times q^n

De manière générale, si pp est un entier naturel, on a :

un=up×qn−pu_n=u_p\times q^{n-p}

Remarque :
On peut se donner une démonstration un peu "intuitive du résultat", il suffit de calculer les premiers termes de la suite en prenant en compte la remarque précédente :

u1=u0×qu_1=u_0\times q

u2=u1×q=u0×q×q=u0×q2u_2=\textcolor{red}{u_1}\times q=\textcolor{red}{u_0\times q}\times q=u_0\times q^2

u3=u2×q=u0×q2×q=u0×q3u_3=\textcolor{red}{u_2}\times q=\textcolor{red}{u_0\times q^2}\times q=u_0\times q^3

u4=u3×q=u0×q3×q=u0×q4u_4=\textcolor{red}{u_3}\times q=\textcolor{red}{u_0\times q^3}\times q=u_0\times q^4

... et ainsi de suite, de manière à trouver la formule générale.

Propriété : variations d'une suite géométrique.
Soit qq un réel et (un)(u_n) une suite géométrique de raison qq.

  • Si q>1q>1, alors la suite est croissante si u0>0u_0>0 et décroissante si u0<0u_0<0 ;
  • Si q<1q<1, alors la suite est décroissante si u0>0u_0>0 et croissante si u0<0u_0<0.

3. Somme des premiers termes d'une suite géométrique.

Théorème :
Soit nn un entier naturel différent de 00 et qq un réel différent de 1. On a alors :

1+q+q2+...+qn=1−qn+11−q1+q+q^2+...+q^n=\frac{1-q^{n+1}}{1-q}

Exemple :

1+3+32+...+3n=1−3n+11−3=12(3n+1−1)1+3+3^2+...+3^n=\frac{1-3^{n+1}}{1-3}=\frac{1}{2}(3^{n+1}-1)

Théorème :
Soit qq un réel non nul différent de 1 et (un)(u_n) une suite géométrique de raison qq.
Soit nn un entier naturel. On a alors :

u0+u1+...+un⎵n+1 termes=u0×1−qn+11−q\underbrace{u_0+u_1+...+u_n}_{n+1 \textrm{\ termes}}=u_0\times\frac{1-q^{n+1}}{1-q}

Toutes nos vidéos sur les suites en 1ère s



Posez vos questions

D'autres interrogations sur ce cours ? Démarrez une discussion et obtenez des réponses à des exercices pratiques.

Accéder au forum

Fiches méthodes

  1. Représenter graphiquement les termes d'une suite
  2. Factorisation d'un polynôme par identification
  3. Les dérivées des fonctions de référence
  4. L'identification pour une fonction rationnelle
  5. Quelques propriétés de la bissectrice
  6. Sur la dérivation
  7. Formule de la hauteur dans le triangle
  8. Mise en forme canonique et résolution du second degré
  9. Nombre dérivé et fonction dérivée
  10. Trouver deux nombres à somme et produit fixés
  11. La loi des sinus
  12. Évolutions en pourcentages
  13. Equations du second degré
  14. Formule de la médiane
  15. Formule d'Al-Kashi (la loi des cosinus)
  16. Résoudre les équations du second degré
  17. Equations du troisième degré
  18. Forme canonique d'un polynôme du second degré
  19. Les suites arithmétiques en 1ere
  20. Les suites numériques
  21. Introduction aux suites géométriques

Cours de mathématiques de première S

  1. Rappels pour une 1ère S
  2. Le second degré (1ère partie)
  3. Le second degré (2ème partie)
  4. Les suites en 1ère S
  5. Les fonctions de référence
  6. Fonctions dérivées en 1ère S
  7. Trigonométrie en 1ère S
  8. Barycentre
  9. Probabilités en 1ère S
  10. Modélisation et échantillonnage en 1ère S
  11. Statistiques en 1ère S
  12. Produit scalaire et applications en 1ère S
6ème 5ème 4ème 3ème
2nde 1ère S 1ère ES 1ère L
Term S Term ES Term L
Prépa HEC Maths SUP Maths SPE
Hors Programme Outils mathématiques