Formule de la médiane en Première S
On suppose connue la loi des cosinus (formule d’Al-Kashî), dont l’énoncé est rappelé ci-dessous.
Théorème 1 (Loi des cosinus).
Dans tout triangle ABC, on a BC2=AB2+AC2−2×AB×AC×cosBAC.
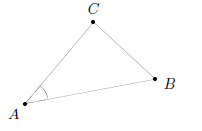
Cette relation permet de calculer la longueur d’une médiane à partir des côtés dans un triangle.
Théorème 2 (Formule de la médiane).
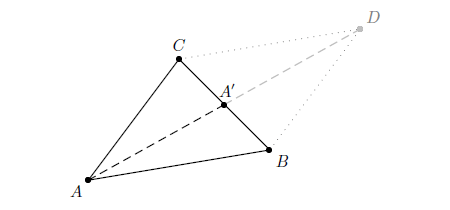
Dans un triangle ABC avec A′ milieu de [BC], on a : 4×AA′2=2×AB2+2×AC2−BC2.
Démonstration.
Avec D symétrique de A par rapport à A′, la loi des cosinus dans ABD donne :
AD2=AB2+BD2−2×AB×BD×cosABD.
Or, on a BD=AC,AD=2×AA′ et ABD=180−BAC ; donc 4×AA′2=AB2+AC2+2×AB×AC×cosBAC, puisque deux angles supplémentaires ont des cosinus opposés.
Dans le triangle ABC, la loi des cosinus donne 2×AB×AC×cosBAC=AB2+AC2−BC2.
On en déduit donc : 4×AA′2=2×AB2+2×AC2−BC2.
Corollaire 1.
Avec les notations traditionnelles (a, b, c et mA) dans le triangle, on a :
mA2=2b2+c2−4a2
Par Zauctore
Toutes nos vidéos sur formule de la médiane

