Calcul barycentrique
Classe de Première.
Cours (sans démonstration) rappelant l'essentiel sur les barycentres.
1 - Introduction
Deux masses, l’une de kg et l’autre de kg, sont fixées aux extrémités d’une barre comme représenté ci-dessous.
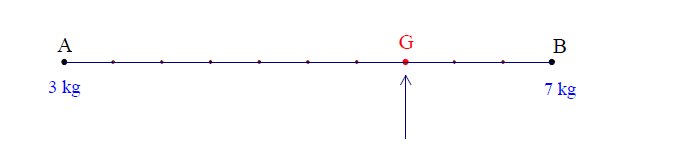
Le point d’équilibre de cette barre est le point où s’équilibrent les forces exercées par ces masses ; celui-ci doit être tel que :
C'est-à-dire :
Ce qui se traduit (après calculs) par :
Cette égalité détermine parfaitement la position d'équilibre de la barre.
2 - Définitions
Soient et deux points points pondérés- c’est-à-dire affectés d’un coefficient : est le coefficient de , est celui de .
Théorème 1
Si , alors il existe un unique point tel que :
Définition 1
Lorsqu’il existe, ce point unique est appelé barycentre du
système de points pondérés et .
Remarque. Lorsque , il n’est pas possible de définir le barycentre de et .
On retiendra, lorsque
Le théorème et la définition s’étendent au cas d’un système de trois points pondérés , et , lorsque .
Dans ce cas, on a l’existence et l’unicité du point G tel que :
De la même manière, si , alors il existe un et un seul point tel que
3 - Propriétés
Propriété 1 (Position)
_Pour , est le barycentre de et
, si, et seulement si
De même, on a :
Le barycentre de deux points et est donc aligné avec ceux-ci ; inversement, tout point situé sur la droite peut être vu comme un barycentre de et . Lorsque l’on a et alors est situé sur le segment (privé de ses extrémités)._
La propriété s’étend au cas d’un nombre fini quelconque de points pondérés dont la somme des coefficients est non-nulle. Dans le cas de trois points, si , alors :
Tout barycentre de trois points (non-alignés) est situé dans le plan défini par ceux-ci.
La réciproque est vraie. Lorsque l’on a , et , alors est à l’intérieur du triangle .
La propriété découle de la relation de Chasles, appliquée dans la définition du barycentre.
C’est cette propriété qui permet de construire le barycentre de deux ou trois points.
Propriété 2 (Condensation, réduction)
Pour , est le barycentre de et , si, et seulement si, pour tout point , on a :
Cette propriété s’étend à plusieurs points : si , le barycentre de est caractérisé par le fait que, pour tout :
La Propriété 2 est une conséquence de la relation de Chasles.
Cette propriété permet de réduire certaines sommes vectorielles (voir l’exemple type en fin d’article).
Propriété 3 (Linéarité)
Soit le barycentre de et , avec .
Alors pour tout , est aussi le barycentre de et , ou même de et .
Cela signifie que l’on peut multiplier tous les coefficients (ou les diviser) par un même nombre non-nul sans changer le barycentre.
Cette propriété s’étend à un nombre fini quelconque de points.
Propriété 4 (Associativité)
Soit le barycentre de , et , avec . Si , alors le barycentre de et existe et dans ce cas, est encore le barycentre de et .
C’est-à-dire qu’on peut remplacer quelques points par leur barycentre (partiel), à condition de l’affecter de la somme de leurs coefficients.
Cette propriété s’´etend à un nombre fini quelconque de points.
Ceci permet de construire le barycentre de plusieurs points.
Cas particulier.
Le milieu d’un segment est en fait le barycentre de et , ou même de , , pour tout .
C’est l’isobarycentre des points et .
Cette notion s’étend au cas d’un nombre fini quelconque de points.
Dans le cas de trois points , et , on retrouve
le centre de gravité du triangle .
Exemple-type
1. Trouver tous les points du plan tels que :
Avec le barycentre de et , on obtient d’après la propriété 2 (propriété de réduction)
ce qui définit le cercle de centre et de rayon .
2. Trouver tous les points du plan tels que
Avec les barycentres
– de et
– de etOn peut réduire ceci à l’aide de la propriété 2.
Ce qui définit la médiatrice du segment .
Par Zauctore
Toutes nos vidéos sur barycentre