Cercle trigonométrique

par Zorro

Cette fiche permet de trouver rapidement les sinus et les cosinus des principaux angles remarquables, en les lisant directement sur le cercle trigonométrique.

Pour résoudre bon nombre d'exercices, il faut être capable de trouver rapidement les sinus et cosinus de certains angles.

L'image que vous voyez vous permet d'y répondre :

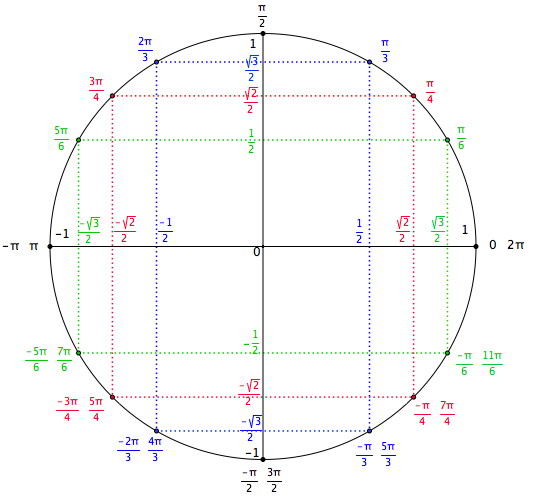
En sachant que les cosinus sont lus sur les axes des abscisses et les sinus sur l'axe des ordonnées, on lit rapidement que :

Il peut être intéressant de savoir reconstruire ce cercle.

Pour cela il faut commencer par mettre, sur les axes, les valeurs dans l'ordre croissant

$\frac{1}{2}$ , $\frac{\sqrt{2}}{2}$ , $\frac{\sqrt{3}}{2}$

Et faire de même avec les valeurs négatives.

Il ne reste plus qu'à construire les rectangles bleus, rouges et verts.

Les points du cercle sont alors reportés dans l'ordre croissant :

$\frac{\pi}{6}$, $\frac{\pi}{4}$ , $\frac{\pi}{3}$, etc...

Et pour ceux qui veulent aller plus loin, rendez-vous sur le site des Cours Thierry avec un cours complet sur le sujet.

Toutes nos vidéos sur cercle trigonométrique : le cours ultime