Le théorème d’Aubry
Plan de cours
Voici un court article exposant la preuve essentiellement géométrique du théorème d'Aubry sur les sommes de deux carrés, reconstruite d'après un instructif paragraphe de l'un des livres d'arithmétique de M. Guinot.
Enoncé
Le théorème d'Aubry s'énonce ainsi dans le cas de deux carrés :
Lorsqu'il un nombre entier s'écrit comme une somme de deux carrés de nombres rationnels, il s'écrit aussi nécessairement comme une somme de deux carrés de nombres entiers.
Démonstration
La démonstration concerne la traduction géométrique de cet énoncé :
Lorsque le cercle centré à l'origine et de rayon ( entier) passe par un point dont les coordonnées sont rationnelles, il passe aussi nécessairement par un point dont les coordonnées sont entières.
La preuve reconstruite ici en détail, qui procède par "descente", est à mon avis intéressante par l'éventail des outils élémentaires utilisés.
Introduction
Dans le livre de Marc Guinot, Les resveries de Fermat (Arithmétique pour amateurs, tome 2), on trouve ce théorème, attribué à Aubry (1912) :
Si un nombre entier peut s’écrire comme une somme de deux carrés de nombres rationnels, alors il peut aussi s’écrire comme une somme de deux carrés de nombres entiers.
Ce théorème peut être étendu à des sommes de trois ou même quatre carrés... On se limite dans ce document au cas de deux carrés.
Théorème 1.
Le nombre entier étant fixé, si l’équation admet une solution en nombres rationnels, alors elle admet aussi une solution en nombres entiers.
En voici la traduction géométrique, dans un repère orthonormé.
Théorème 2.
Si le cercle passe par un point à coordonnées rationnelles, alors il passe aussi par un point à coordonnées entières.
Démonstration du théorème 2.
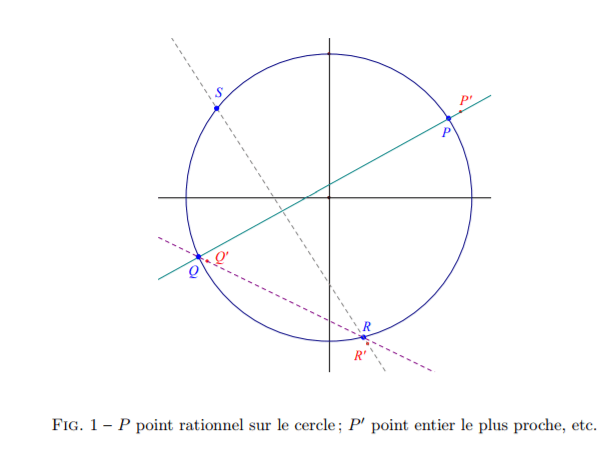
Soit un point ( ; à coordonnées rationnelles (non entières)
sur le cercle et soit un point à coordonnées entières tel que , c’est-à-dire :
Il est clair qu’un tel point existe toujours. La droite coupe en et .
Déterminons les coordonnées de ce point . Le vecteur :
dirige la droite , d’où la caractérisation sous forme paramétrique d’un quelconque point de celle-ci :
En reportant ces expressions dans l’équation de , on obtient :
c’est-à-dire, en ordonnant relativement au paramètre ,
C’est une équation du second degré en , dont est une solution, puisque (correspondant à cette valeur du paramètre) est point d’intersection de la droite et du cercle.
La seconde solution est donc donnée par :
Observons que: ; alors on a plus simplement :
On en déduit alors les coordonnées (rationnelles) du point cherché :
Or, on a :
Ainsi, peut s'écrire comme un quotient d’entiers de la forme
Et puisque le choix de est tel que , alors on en déduit l’inégalité .
En revenant aux coordonnées du point , on a
, ce qui montre qu’elles peuvent s’écrire comme des quotients d’entiers dont le dénominateur est tel que .
Si les coordonnées de ne sont pas entières, alors on recommence le procédé avec point à cordonnées entières le plus proche : la droite recoupe le cercle en , dont les coorodonnées pourront se mettre sous mettre sous la forme d'un quotient d'entiers de dénominateur , avec .
Un tel procédé doit se terminer, sans quoi on produirait ainsi une suite strictement décroissante d’entiers positifs. . . Ainsi, on pourra trouver un point à coordonnées entières sur le cercle .
Par Zauctore